La tirannia dei costi

I costi rappresentano un elemento chiave da considerare per implementare  un buon piano d’investimento.

A differenza dei rendimenti, i costi sono un elemento che possiamo controllare e dunque ottimizzare.

Negli investimenti “i rendimenti sono incerti, i costi però sono certi”.

Di sicuro, minore è il costo da sostenere per l’acquisto e gestione di asset finanziari, maggiore sarà il rendimento finale del nostro investimento.

“You get what you don’t pay for”, ovvero si ottiene ciò che non si spende, come dice Jack Bogle.

L’impatto dei costi può essere devastante soprattutto nel lungo termine. Occorre dunque prestare attenzione per non vanificare anni ed anni dei nostri sudati risparmi.

Infatti, supponiamo di avere 3 piani di investimento , A , B e C . Tutti e 3 partono dalla stessa cifra, per esempio 10.000 Euro.

A,B e C investono nello stesso strumento, ad esempio un indice azionario ben diversificato che produce lo stesso rendimento, ovvero 7% composto annuo per 30 anni.

Applicando la magia della capitalizzazione composta, il risultato finale al lordo delle commissioni è di 76.122.55 Euro.

Vediamo ora il risultato al netto dei costi , considerando 3 scenari possibili :

A) Costo del 1%;

B) Costo del 2%;

C) Costo del 3%.

Bene, il risultato è il seguente:

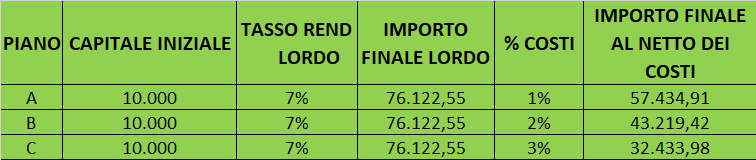
Come si evince dalla tabella , un costo del 3% produce effetti devastanti nel rendimento finale del nostro investimento, andando a più che dimezzare il suo valore finale.

Nel caso di considerare un 2% di costo, il valore finale che si ottiene è di 43.219,42.

“Spendere” un 1% in meno annuo di costi si traduce dunque in un “guadagno” ulteriore di oltre 10.000 Euro.

Concludendo , una buona pianificazione finanziaria non può esimersi dal considerare i costi che si applicano al proprio piano. Un attenta gestione ed ottimizzazione dei costi consente di diminuire il tempo necessario per raggiungere il proprio obiettivo finanziario.

“Cost matters, and matters a lot “!!! Un piccolo foro in una nave può difatti farla affondare col passare del tempo……….